Navigation

Dimensionality Reduction

Linear Discriminant Analysis (LDA)

class mlpy.LDA(method='cov')

Linear Discriminant Analysis.

Initialization.

Parameters :
method : str

‘cov’ or ‘fast’
coeff()

Returns the tranformation matrix (P,C-1), where C is the number of classes. Each column contains coefficients for one transformation vector.

learn(x, y)

Computes the transformation matrix. x is a matrix (N,P) and y is a vector containing the class labels. Each column of x represents a variable, while the rows contain observations.

transform(t)

Embed t (M,P) into the C-1 dimensional space. Returns a (M,C-1) matrix.

Example:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> mean1, cov1, n1 = [1, 4.5], [[1,1],[1,2]], 20  # 20 samples of class 1
>>> x1 = np.random.multivariate_normal(mean1, cov1, n1)
>>> y1 = np.ones(n1, dtype=np.int)
>>> mean2, cov2, n2 = [2.5, 2.5], [[1,1],[1,2]], 30 # 30 samples of class 2
>>> x2 = np.random.multivariate_normal(mean2, cov2, n2)
>>> y2 = 2 * np.ones(n2, dtype=np.int)
>>> x = np.concatenate((x1, x2), axis=0) # concatenate the samples
>>> y = np.concatenate((y1, y2))
>>> lda = mlpy.LDA()
>>> lda.learn(x, y) # compute the tranformation matrix
>>> z = lda.transform(x) # embedded x into the C-1 = 1 dimensional space

Spectral Regression Discriminant Analysis (SRDA)

class mlpy.SRDA(alpha=0.001)

Spectral Regression Discriminant Analysis.

Initialization.

Parameters :
alpha : float (>=0)

regularization parameter
coeff()

Returns the tranformation matrix (P,C-1), where C is the number of classes. Each column contains coefficients for one transformation vector.

learn(x, y)

Computes the transformation matrix. x is a matrix (N,P) and y is a vector containing the class labels. Each column of x represents a variable, while the rows contain observations.

transform(t)

Embed t (M,P) into the C-1 dimensional space. Returns a (M,C-1) matrix.

Kernel Fisher Discriminant Analysis (KFDA)

class mlpy.KFDA(lmb=0.001, kernel=None)

Kernel Fisher Discriminant Analysis.

Initialization.

Parameters :
lmb : float (>= 0.0)

regularization parameter

kernel : None or mlpy.Kernel object.

if kernel is None, K and Kt in .learn() and in .transform() methods must be precomputed kernel matricies, else K and Kt must be training (resp. test) data in input space.
coeff()

Returns the tranformation vector (N,1).

learn(K, y)

Computes the transformation vector.

Parameters :
K: 2d array_like object

precomputed training kernel matrix (if kernel=None); training data in input space (if kernel is a Kernel object)

y : 1d array_like object integer (N)

class labels (only two classes)
transform(Kt)

Embed Kt into the 1d kernel fisher space.

Parameters :
Kt : 1d or 2d array_like object

precomputed test kernel matrix. (if kernel=None); test data in input space (if kernel is a Kernel object).

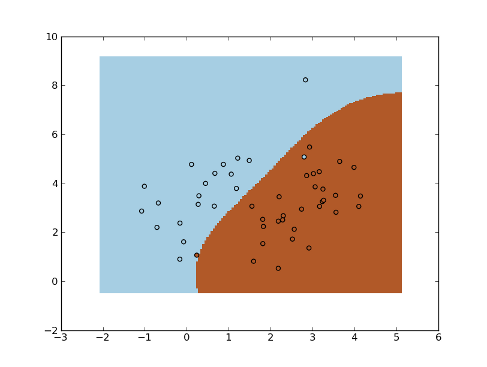
Example - KNN in kernel fisher space:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> mean1, cov1, n1 = [1, 4.5], [[1,1],[1,2]], 20  # 20 samples of class 1
>>> x1 = np.random.multivariate_normal(mean1, cov1, n1)
>>> y1 = np.ones(n1, dtype=np.int)
>>> mean2, cov2, n2 = [2.5, 2.5], [[1,1],[1,2]], 30 # 30 samples of class 2
>>> x2 = np.random.multivariate_normal(mean2, cov2, n2)
>>> y2 = 2 * np.ones(n2, dtype=np.int)
>>> x = np.concatenate((x1, x2), axis=0) # concatenate the samples
>>> y = np.concatenate((y1, y2))
>>> K = mlpy.kernel_gaussian(x, x, sigma=3) # compute the kernel matrix
>>> kfda = mlpy.KFDA(lmb=0.01)
>>> kfda.learn(K, y) # compute the tranformation vector
>>> z = kfda.transform(K) # embedded x into the kernel fisher space
>>> knn = mlpy.KNN(k=5)
>>> knn.learn(z, y) # learn KNN in the kernel fisher space
>>> xmin, xmax = x[:,0].min()-1, x[:,0].max()+1
>>> ymin, ymax = x[:,1].min()-1, x[:,1].max()+1
>>> xx, yy = np.meshgrid(np.arange(xmin, xmax, 0.05), np.arange(ymin, ymax, 0.05))
>>> xt = np.c_[xx.ravel(), yy.ravel()]
>>> Kt = mlpy.kernel_gaussian(xt, x, sigma=3) # compute the kernel matrix Kt
>>> zt = kfda.transform(Kt) # embedded xt into the kernel fisher space
>>> yt = KNN.pred(zt).reshape(xx.shape) # perform the KNN prediction in the kernel fisher space
>>> fig = plt.figure(1)
>>> cmap = plt.set_cmap(plt.cm.Paired)
>>> plot1 = plt.pcolormesh(xx, yy, yt)
>>> plot2 = plt.scatter(x[:,0], x[:,1], c=y)
>>> plt.show()
_images/kfda.png

Principal Component Analysis (PCA)

class mlpy.PCA(method='svd', whiten=False)

Principal Component Analysis.

Initialization.

Parameters :
method : str

method, ‘svd’ or ‘cov’

whiten : bool

whitening. The eigenvectors will be scaled by eigenvalues**-(1/2)
coeff()

Returns the tranformation matrix (P,L), where L=min(N,P), sorted by decreasing eigenvalue. Each column contains coefficients for one principal component.

coeff_inv()

Returns the inverse of tranformation matrix (L,P), where L=min(N,P), sorted by decreasing eigenvalue.

evals()

Returns sorted eigenvalues (L), where L=min(N,P).

learn(x)

Compute the principal component coefficients. x is a matrix (N,P). Each column of x represents a variable, while the rows contain observations.

transform(t, k=None)

Embed t (M,P) into the k dimensional subspace. Returns a (M,K) matrix. If k =None will be set to min(N,P)

transform_inv(z)

Transform data back to its original space, where z is a (M,K) matrix. Returns a (M,P) matrix.

Example:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> mean, cov, n = [0, 0], [[1,1],[1,1.5]], 100
>>> x = np.random.multivariate_normal(mean, cov, n)
>>> pca.learn(x)
>>> coeff = pca.coeff()
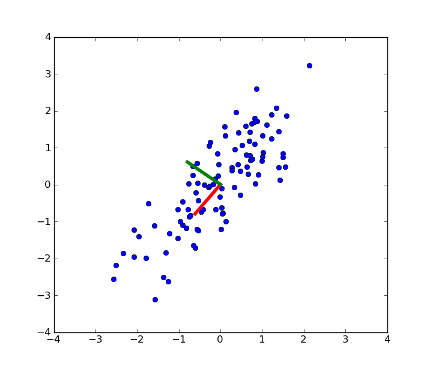
>>> fig = plt.figure(1) # plot
>>> plot1 = plt.plot(x[:, 0], x[:, 1], 'o')
>>> plot2 = plt.plot([0,coeff[0, 0]], [0, coeff[1, 0]], linewidth=4, color='r') # first PC
>>> plot3 = plt.plot([0,coeff[0, 1]], [0, coeff[1, 1]], linewidth=4, color='g') # second PC
>>> xx = plt.xlim(-4, 4)
>>> yy = plt.ylim(-4, 4)
>>> plt.show()
_images/pca.png 
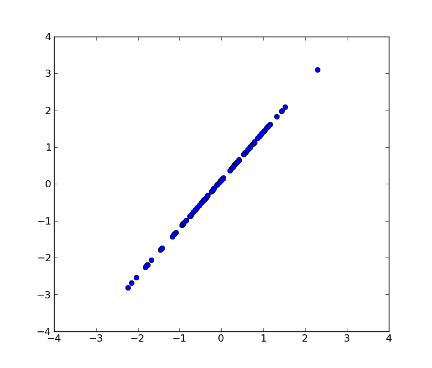
>>> z = pca.transform(x, k=1) # transform x using the first PC
>>> xnew = pca.transform_inv(z) # transform data back to its original space
>>> fig2 = plt.figure(2) # plot
>>> plot1 = plt.plot(xnew[:, 0], xnew[:, 1], 'o')
>>> xx = plt.xlim(-4, 4)
>>> yy = plt.ylim(-4, 4)
>>> plt.show()
_images/pca2.png

Fast Principal Component Analysis (PCAFast)

Fast PCA implementation described in [Sharma07].

class mlpy.PCAFast(k=2, eps=0.01)

Fast Principal Component Analysis.

Initialization.

Parameters :
k : integer

the number of principal axes or eigenvectors required

eps : float (> 0)

tolerance error
coeff()

Returns the tranformation matrix (P,K) sorted by decreasing eigenvalue. Each column contains coefficients for one principal component.

coeff_inv()

Returns the inverse of tranformation matrix (K,P), sorted by decreasing eigenvalue.

learn(x)

Compute the firsts k principal component coefficients. x is a matrix (N,P). Each column of x represents a variable, while the rows contain observations.

transform(t)

Embed t (M,P) into the k dimensional subspace. Returns a (M,K) matrix.

transform_inv(z)

Transform data back to its original space, where z is a (M,K) matrix. Returns a (M,P) matrix.

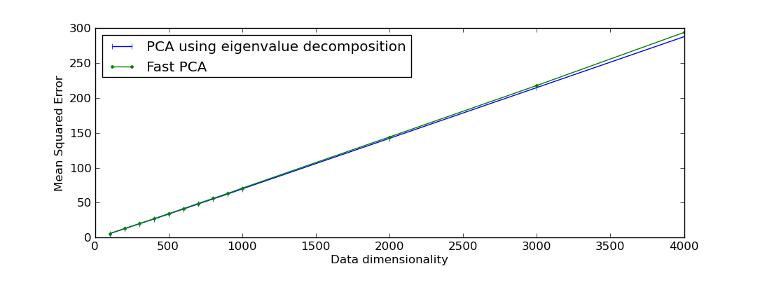
Example reproducing Figure 1 of [Sharma07]:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> h = 10 # dimension reduced to h=10
>>> n = 100 # number of samples
>>> d = np.array([100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000]) # number of dimensions
>>> mse_eig, mse_fast = np.zeros(len(d)), np.zeros(len(d))
>>> pca = mlpy.PCA(method='cov') # pca (eigenvalue decomposition)
>>> pca_fast=  mlpy.PCAFast(k=h) # fast pca
>>> for i in range(d.shape[0]):
...     x = np.random.rand(n, d[i])
...     pca.learn(x) # pca (eigenvalue decomposition)
...     y_eig = pca.transform(x, k=h) # reduced dimensional feature vectors
...     xhat_eig = pca.transform_inv(y_eig) # reconstructed vector
...     pca_fast.learn(x) # pca (eigenvalue decomposition)
...     y_fast = pca_fast.transform(x) # reduced dimensional feature vectors
...     xhat_fast = pca_fast.transform_inv(y_fast) # reconstructed vector
...     for j in range(n):
...         mse_eig[i] += np.sum((x[j] - xhat_eig[j])**2)
...         mse_fast[i] += np.sum((x[j] - xhat_fast[j])**2)
...     mse_eig[i] /= n
...     mse_fast[i] /= n
...
>>> fig = plt.figure(1)
>>> plot1 = plt.plot(d, mse_eig, '|-b', label="PCA using eigenvalue decomposition")
>>> plot2 = plt.plot(d, mse_fast, '.-g', label="Fast PCA")
>>> leg = plt.legend(loc = 'best')
>>> xl = plt.xlabel("Data dimensionality")
>>> yl = plt.ylabel("Mean Squared Error")
>>> plt.show()
_images/fastpca.png

Kernel Principal Component Analysis (KPCA)

class mlpy.KPCA(kernel=None)

Kernel Principal Component Analysis.

Initialization.

Parameters :
kernel : None or mlpy.Kernel object.

if kernel is None, K and Kt in .learn() and in .transform() methods must be precomputed kernel matricies, else K and Kt must be training (resp. test) data in input space.
coeff()

Returns the tranformation matrix (N,N) sorted by decreasing eigenvalue.

evals()

Returns sorted eigenvalues (N).

learn(K)

Compute the kernel principal component coefficients.

Parameters :
K: 2d array_like object

precomputed training kernel matrix (if kernel=None); training data in input space (if kernel is a Kernel object)
transform(Kt, k=None)

Embed Kt into the k dimensional subspace.

Parameters :
Kt : 1d or 2d array_like object

precomputed test kernel matrix. (if kernel=None); test data in input space (if kernel is a Kernel object).

Example:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mlpy
>>> np.random.seed(0)
>>> np.random.seed(0)
>>> x = np.zeros((150, 2))
>>> y = np.empty(150, dtype=np.int)
>>> theta = np.random.normal(0, np.pi, 50)
>>> r = np.random.normal(0, 0.1, 50)
>>> x[0:50, 0] = r * np.cos(theta)
>>> x[0:50, 1] = r * np.sin(theta)
>>> y[0:50] = 0
>>> theta = np.random.normal(0, np.pi, 50)
>>> r = np.random.normal(2, 0.1, 50)
>>> x[50:100, 0] = r * np.cos(theta)
>>> x[50:100, 1] = r * np.sin(theta)
>>> y[50:100] = 1
>>> theta = np.random.normal(0, np.pi, 50)
>>> r = np.random.normal(5, 0.1, 50)
>>> x[100:150, 0] = r * np.cos(theta)
>>> x[100:150, 1] = r * np.sin(theta)
>>> y[100:150] = 2
>>> cmap = plt.set_cmap(plt.cm.Paired)
>>> gK = mlpy.kernel_gaussian(x, x, sigma=2) # gaussian kernel matrix
>>> pK = mlpy.kernel_polynomial(x, x, gamma=1.0, b=1.0, d=2.0) # polynomial kernel matrix
>>> gaussian_pca = mlpy.KPCA()
>>> polynomial_pca = mlpy.KPCA()
>>> gaussian_pca.learn(gK)
>>> polynomial_pca.learn(pK)
>>> gz = gaussian_pca.transform(gK, k=2)
>>> pz = polynomial_pca.transform(pK, k=2)
>>> fig = plt.figure(1)
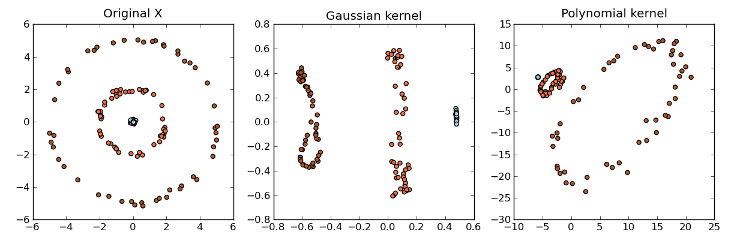
>>> ax1 = plt.subplot(131)
>>> plot1 = plt.scatter(x[:, 0], x[:, 1], c=y)
>>> title1 = ax1.set_title('Original X')
>>> ax2 = plt.subplot(132)
>>> plot2 = plt.scatter(gz[:, 0], gz[:, 1], c=y)
>>> title2 = ax2.set_title('Gaussian kernel')
>>> ax3 = plt.subplot(133)
>>> plot3 = plt.scatter(pz[:, 0], pz[:, 1], c=y)
>>> title3 = ax3.set_title('Polynomial kernel')
>>> plt.show()
_images/kernel_pca.png
[Cai08]D Cai, X He, J Han. SRDA: An Efficient Algorithm for Large-Scale Discriminant Analysis. Knowledge and Data Engineering, IEEE Transactions on Volume 20, Issue 1, Jan. 2008 Page(s):1 - 12.
[Sharma07](1, 2) A Sharma, K K Paliwal. Fast principal component analysis using fixed-point algorithm. Pattern Recognition Letters 28 (2007) 1151–1155.
[Mika99]S Mika et al. Fisher Discriminant Analysis with Kernels. Neural Networks for Signal Processing IX, 1999. Proceedings of the 1999 IEEE Signal Processing Society Workshop.
[Scholkopf96]B Scholkopf, A Smola, KR Muller. Nonlinear Component Analysis as a Kernel EigenValue Problem

Table Of Contents

Previous topic

Feature Selection

Next topic

Cross Validation

This Page

Navigation

© Copyright 2011, mlpy Developers. Created using Sphinx 1.0.7.